聚类

什么样的聚类效果好？

聚类结果的簇内相似度高，且簇间相似度低

聚类性能度量

外部指标：结果与某个参考模型作比较，如Jaccard系数，FM指数，Rand指数，
内部指标：直接考察聚类结果，如DB指数，DI指数

计算距离

闵可夫斯基距离和VDM距离结合，可以计算有序属性和无序属性

sklearn聚类

  • 参考：
  • scikit-learn主要由分类、回归、聚类和降维四大部分组成，其中分类和回归属于有监督学习范畴，聚类属于无监督学习范畴，降维适用于有监督学习和无监督学习。scikit-learn的结构示意图如下所示：
  • img
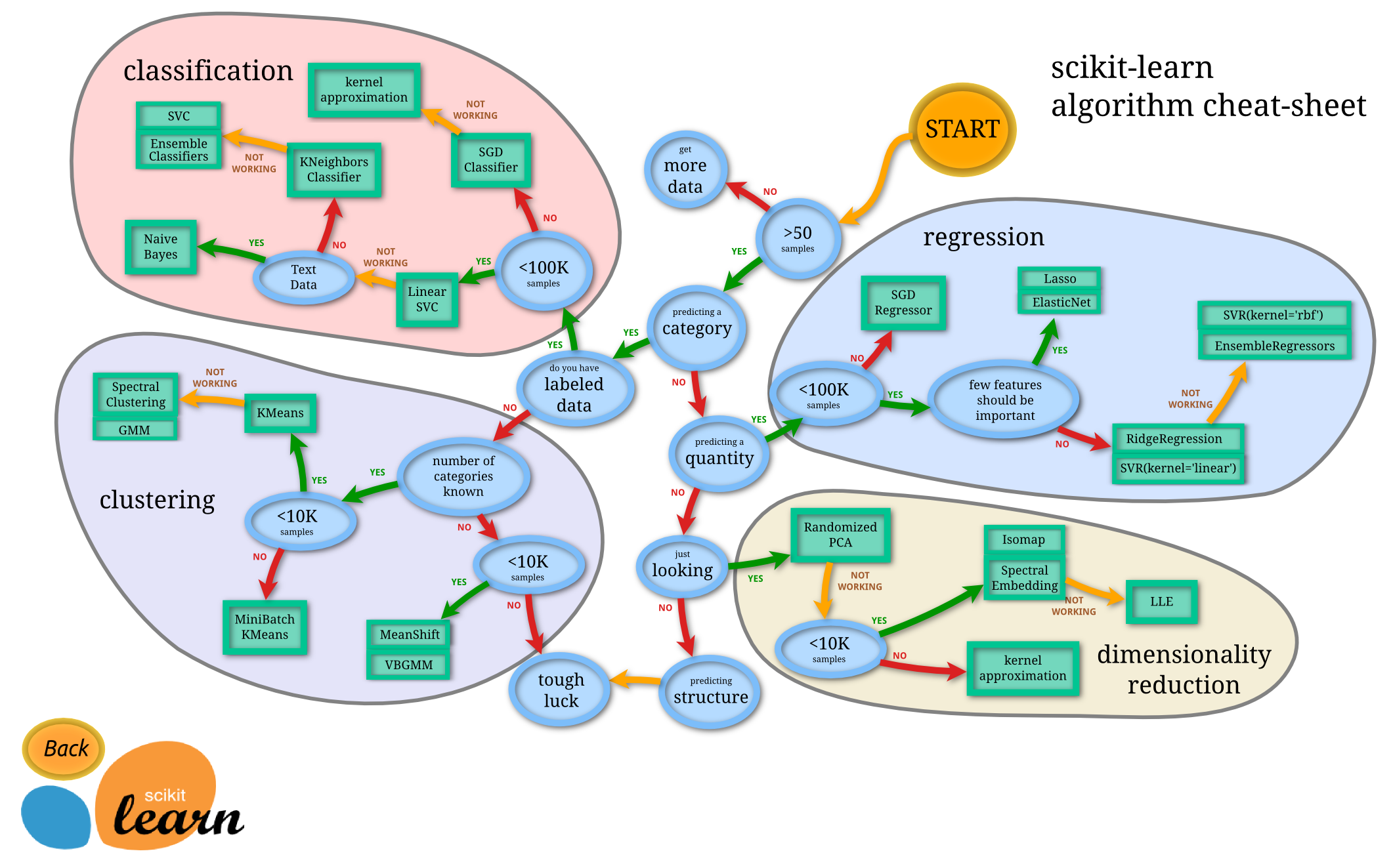
  • scikit-learn中的聚类算法主要有：
    • K-Means(cluster.KMeans)
    • AP聚类（cluster.AffinityPropagation）
    • 均值漂移（cluster.MeanShift）
    • 层次聚类（cluster.AgglomerativeClustering）
    • DBSCAN（cluster.DBSCAN）
    • BRICH（cluster.Brich）
    • 谱聚类（cluster.Spectral.Clustering）
    • 高斯混合模型（GMM）∈期望最大化（EM）算法（mixture.GaussianMixture）

K-Means

1.1 算法描述

  1. 随机选择k个中心
  2. 遍历所有样本，把样本划分到距离最近的一个中心
  3. 划分之后就有K个簇，计算每个簇的平均值作为新的质心
  4. 重复步骤2，直到达到停止条件
  • 停止条件：
    • 聚类中心不再发生变化；所有的距离最小；迭代次数达到设定值，
  • 代价函数：误差平方和

1.2 算法优缺点

优点：

  • 算法容易理解，聚类效果不错
  • 具有出色的速度
  • 当簇近似高斯分布时，效果比较好

缺点：

  • 需要自己确定K值,k值的选定是比较难确定
  • 对初始中心点敏感
  • 不适合发现非凸形状的簇或者大小差别较大的簇
  • 特殊值/离群值对模型的影响比较大
  • 从数据先验的角度来说，在 Kmeans 中,我们假设各个 cluster 的先验概率是一样的,但是各个 cluster 的数据量可能是不均匀的。举个例子,cluster A 中包含了10000个样本,cluster B 中只包含了100个。那么对于一个新的样本,在不考虑其与A cluster、 B cluster 相似度的情况,其属于 cluster A 的概率肯定是要大于 cluster B的。

1.3 效果评价

聚类结果的簇内相似度高，且簇间相似度低

常见方法有轮廓系数Silhouette Coefficient和Calinski-Harabasz Index(CH指标，越大越好)

Silhouette Coefficient：

$$s(i)=\frac{b(i)-a(i)}{max(a(i),b(i))}$$

其中a(i)是样本$i$到同类所有样本的平均距离，b(i)是到其他某类所有样本的平均距离

  • si接近1，则说明样本i聚类合理；
  • si接近-1，则说明样本i更应该分类到另外的簇；
  • 若si 近似为0，则说明样本i在两个簇的边界上。

Calinski-Harabasz Index

类别内部数据的协方差越小越好，类别之间的协方差越大越好，这样的Calinski-Harabasz分数会高。实例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
"""
下面的方法是用kmeans方法进行聚类，用calinski_harabaz_score方法评价聚类效果的好坏
大概是类间距除以类内距，因此这个值越大越好
"""
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn import metrics
"""
下面是生成一些样本数据
X为样本特征，Y为样本簇类别， 共1000个样本，每个样本2个特征，共4个簇，簇中心在[-1,-1], [0,0],[1,1], [2,2]，
簇方差分别为[0.4, 0.5, 0.2]
"""
X, y = make_blobs(n_samples=500, n_features=2, centers=[[2,3], [3,0], [1,1]], cluster_std=[0.4, 0.5, 0.2],
                  random_state =9)
"""
首先画出生成的样本数据的分布
"""
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()
"""
下面看不同的k值下的聚类效果
"""
score_all=[]
list1=range(2,6)
#其中i不能为0，也不能为1
for i in range(2,6):
    y_pred = KMeans(n_clusters=i, random_state=9).fit_predict(X)
    #画出结果的散点图
    plt.scatter(X[:, 0], X[:, 1], c=y_pred)
    plt.show()
    score=metrics.calinski_harabasz_score(X, y_pred)
    score_all.append(score)
    print(score)
"""
画出不同k值对应的聚类效果
"""
plt.plt(list1,score_all)
plt.show()

python实现KMeans

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import pandas as pd
import numpy as np
from sklearn.preprocessing import LabelEncoder,OneHotEncoder
def random_k_sample(data, k):
    """
    随机选择K个样本作为初始均值向量
    """
    n = np.shape(data)[1] # n个特征
    m = np.shape(data)[0]
    centroids = np.zeros((k, n)) # k个样本
    temp = random.sample(range(m), k)
    for i in range(k):
        centroids[i] = data[temp[i]]
    
    return centroids
## 数据加载过程省略
my_data = data.iloc[:, 0:-1]
my_data = my_data.values
def calc_dist(vec1, vec2):
    """
    计算欧式距离
    """
    return np.sqrt(np.sum(np.power(vec1 - vec2, 2)))
m = np.shape(my_data)[0]
n = np.shape(my_data)[1]
k = 3
centroids = random_k_sample(my_data, k)
# 每个样本与选出来的样本向量计算距离，距离谁近就归为哪一类
result = np.zeros((m, 2)) # 存放样本类别，和到质心的距离
# 控制均值向量是否更新
changed = True
while (changed):
    for i in range(m):
        min_value = np.inf # 最小距离
        min_label = -1 # 类别
        for j in range(k):
            dist = calc_dist(my_data[i], centroids[j])
            if dist < min_value:
                min_value = dist
                min_label = j
        
        result[i, :] = min_value, min_label
        print('iteration %d, %s' % (i, result[i, :]))
    
    is_update = False
    for j in range(k):
        # 计算新的均值向量
        # 对每一类的特征列求平均值
        temp = np.mean(my_data[(result[:, 1] == j)], axis=0)
        
#         print(temp)
#         print(centroids[j])
        # 如果均值向量更新了，重新迭代
        if (centroids[j] != temp).any():
            centroids[j] = temp
            print('update')
            is_update = True
    
    if is_update:
        changed = True
    else:
        changed = False
data['label'] = result[:, 1]

LVQ算法

学习向量量化，随机选择有标记训练样本，找出距离最近的原型向量，根据两者的类别标记是否相同来对原型向量进行相应的更新（靠拢或者远离）。

高斯混合聚类

初始化模型参数，计算各混合分布的后验概率，重新计算新均值向量，新协方差矩阵，新混合系数，不断迭代。

密度聚类算法

DBSCAN

基于密度的空间聚类方法

簇：由密度可达关系导出的最大的密度相连样本集合。
DBSCAN的聚类是一个不断生长的过程。先找到一个核心对象，从整个核心对象出发，找出它的直接密度可达的对象，再从这些对象出发，寻找它们直接密度可达的对象，一直重复这个过程，直至最后没有可寻找的对象了，那么一个簇的更新就完成了。也可以认为，簇是所有密度可达的点的集合。

两个参数：

    • Eps邻域半径(epsilon,小量，小的值）
    • MinPts(minimum number of points required to form a cluster)定义核心点时的阈值。

几个概念：

  • $\epsilon$ 邻域: 对于样本$x_j$，包含D中与$x_j$样本距离不大于$\epsilon$的样本

  • 核心对象：对于任一样本点，如果其 $\epsilon$ 邻域内至少包含MinPts个样本点，那么这个样本点就是核心对象。（一个点）

  • 直接密度可达：如果一个样本点p处于一个核心对象q的Eps邻域内，则称该样本点p从对象q出发时是直接密度可达的。
  • 密度相连：对于样本点p和q，如果存在核心对象m,使得p、p均由m直接密度可达，则称p和q密度相连。

优点：

  • 不需要指定cluster的数目
  • 聚类的形状可以是任意的
  • 能找出数据中的噪音，对噪音不敏感
  • 算法应用参数少，只需要两个
  • 聚类结果几乎不依赖于节点的遍历顺序

缺点：

  • 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。
  • DBSCAN算法的聚类效果依赖于距离公式的选取，实际中常用的距离是欧几里得距离，由于‘维数灾难’，距离的度量标准已变得不再重要。（分类器的性能随着特征数量的增加而不断提升，但过了某一值后，性能不升反而下降，这种现象称为维数灾难。对于维度灾难的理解：维度灾难的理解）
  • 不适合数据集中密度差异很大的情形，因为这种情形，参数Eps,MinPts不好选择。（个人理解，如果是密度大的，你选一个小的邻域半径就可以把这些数据点聚类，但对于那些密度小的数据点，你设置的小的邻域半径，并不能把密度小的这些点给全部聚类。）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_blobs
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle
from sklearn.preprocessing import StandardScaler
# 产生随机数据的中心
centers = [[1, 1], [1, -1], [1, -1]]
n_samples= 500
X, label_true = make_blobs(n_samples=n_samples, centers=centers,
                           cluster_std=0.4, random_state=0)
# 设置密度聚类, 默认是欧式距离
model = DBSCAN(eps=0.3, min_samples=10)
# 自定义函数
#DB = DBSCAN(eps=400,min_samples=min_samples_num, metric=lambda a, b: haversine(a,b)).fit(X)
model.fit(X)
core_samples_mask = np.zeros_like(label_true, dtype=np.bool)
'''
   这里是关键点(针对这行代码：xy = X[class_member_mask & ~core_samples_mask])：
   db.core_sample_indices_  表示的是某个点在寻找核心点集合的过程中暂时被标为噪声点的点(即周围点
   小于min_samples)，并不是最终的噪声点。在对核心点进行联通的过程中，这部分点会被进行重新归类(即标签
   并不会是表示噪声点的-1)，也可也这样理解，这些点不适合做核心点，但是会被包含在某个核心点的范围之内
'''
core_samples_mask[model.core_sample_indices_] = True
##每个数据的分类
label = model.labels_
##分类个数：lables中包含-1，表示噪声点
n_clusters_ =len(np.unique(label)) - (1 if -1 in label else 0)
##绘图
unique_labels = set(label)
'''
   1)np.linspace 返回[0,1]之间的len(unique_labels) 个数
   2)plt.cm 一个颜色映射模块
   3)生成的每个colors包含4个值，分别是rgba
   4)其实这行代码的意思就是生成4个可以和光谱对应的颜色值
'''
colors = plt.cm.Spectral(np.linspace(0, 1, len(unique_labels)))
plt.figure(1)
plt.clf()
for k, col in zip(unique_labels, colors):
    ##-1表示噪声点,这里的k表示黑色
    if k == -1:
        col = 'k'
    ##生成一个True、False数组，lables == k 的设置成True
    class_member_mask = (label == k)
    ##两个数组做&运算，找出即是核心点又等于分类k的值  markeredgecolor='k',
    xy = X[class_member_mask & core_samples_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', c=col,markersize=14)
    '''
       1)~优先级最高，按位对core_samples_mask 求反，求出的是噪音点的位置
       2)& 于运算之后，求出虽然刚开始是噪音点的位置，但是重新归类却属于k的点
       3)对核心分类之后进行的扩展
    '''
    xy = X[class_member_mask & ~core_samples_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', c=col, markersize=6)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()

层次聚类算法

层次聚类试图在不同层次对数据集进行划分，形成树的聚类结构。
AGNES算法在树状图上的特定层次进行分割，得到相应的簇划分结果。

赏

谢谢你请我吃糖果

支付宝
微信

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia-plus根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

怕人询问，咽泪装欢