词向量

2019-12-20

[TOC]

词向量就是把一个词表示成一个向量。简单的方式就是OneHot编码，但是这样做会造成维度灾难，且词与词之间没有关系。另一种方式是用一个向量来表示，维度一般不高，在空间上也可以计算距离来表示词与词之间的相似性。

基本概念

语言模型

语言模型就是给定一个词，预测后面的词在前面的词出现的情况下出现的概率。如果这个概率特别低，说明这句话不是一句自然语言。

$$p(s)=p(w_1)p(w_2|w_1)p(w_3|w_2,w_1)…p(wT|w{T-1} …w_1)$$

$p(w_1)$表示词$w_1$在语料库中出现的概率，考虑一个词前面所有的词来计算概率连乘的话，计算量会特别大，因此采用n-gram模型来进行优化。

n-gram模型

n-gram模型只考虑$w_i$前面的n-1个词，包括$w_i$本身，总共n个词，来计算在给定上文情况下，$w_i$出现的概率。也就是

$$p(w_i|Context_i)=p(wi|w{i-n+1} …w_{i-1})$$

N-gram模型也有些问题，总结如下：

1、n-gram无法建模更远的关系，大部分研究或工作都是使用trigram或bigram；

2、无法建模出词之间的相似度，就是有两个词经常出现在同一个context后面，但是模型是没法体现这个相似性的。

3、有些n元组（n个词的组合，跟顺序有关的）在语料库里面没有出现过，对应出来的条件概率就是0，这样一整句话的概率都是0了，这是不对的，解决的方法主要是两种：平滑法（基本上是分子分母都加一个数）和回退法（利用n-1的元组的概率去代替n元组的概率）

例如：students opened the book

（1）预测的文本 book ，语料库中没有students opened the book 这句话时，book的概率为0；可通过拉普拉斯平滑解决

（2）students opened the 在语料库中不存在时，计算概率值的分母为0；使用opened the 替代，称为backoff。

NNLM

神经网络语言模型使用NN直接取建模概率$p(w_i|Context_i)$,网络的输入是前n-1个单词的向量$C_i$，输出是V个节点，V就是词典大小，其中第$i$个节点的输出值就是$p(w_i|Context_i)$。模型结构如下：

训练的目标是最大似然加正则项：

$$L=max\frac{1}{T}\sum logf(wt,w{t-1},…,w{t-n+2},w{t-n+1};\theta)+R(\theta)$$

其中$\theta$为参数，$R(\theta)$为正则项，输出层采用softmax函数：

$$p(wt|w{t-1} …w{t-n+1})=\frac{e^{y{w_t}}}{\sum e^{y_i}}$$

其中$y_i$是每个输出词$w_i$的log概率，计算如下：

$$y=b+Wx+Utanh(d+Hx)$$

其中$x=(C(w{t-1}),C(w{t-2}),…,C(w_{t-n+1}))$, 输入层x也是要训练的参数，梯度更新的方式为：

$$\theta\leftarrow \theta+\alpha\frac{\partial logp(wt|w{t-1} …w_{t-n+1}))}{\partial \theta}$$

优化结束后，词向量和语言模型就都有了。

CBOW

CBOW是 Continuous Bag Words Model 的缩写，是一种与前向 NNLM 类似的模型，不同点在于 CBOW 去掉了最耗时的非线性隐层且所有词共享。如

CBOW模型是根据上下文预测中心词。

这个网络结构的功能是为了完成一个的事情——判断一句话是否是自然语言。怎么判断呢？使用的是概率，就是计算一下这句话的“一列词的组合”的概率的连乘（联合概率）是多少，如果比较低，那么就可以认为不是一句自然语言，如果概率高，就是一句正常的话。

从输入层到隐层所进行的操作实际就是上下文向量的加和。原始代码如下(变量名也很随意呀)：

// in -> hidden
next_random = next_random * (unsigned long long)25214903917 + 11;
b = next_random % window;
cw = 0;
for (a = b; a < window * 2 + 1 - b; a++) if (a != window) {
    c = sentence_position - window + a;
    if (c < 0) continue;
    if (c >= sentence_length) continue;
    last_word = sen[c];
    if (last_word == -1) continue;
    for (c = 0; c < layer1_size; c++) 
       	neu1[c] += syn0[c + last_word * layer1_size]; // 一维数组存储向量参数
    cw++;
}

其中 sentence_position 为当前 word在句子中下标，b是0~window-1的一个值，整个窗口的大小为$2window+1-2b$，相当于左右给看$window-b$个词。最后将每个词的向量求和，赋值到neu1中

CBOW有两种可选的算法: 层次Softmax和 Negative Sampling。

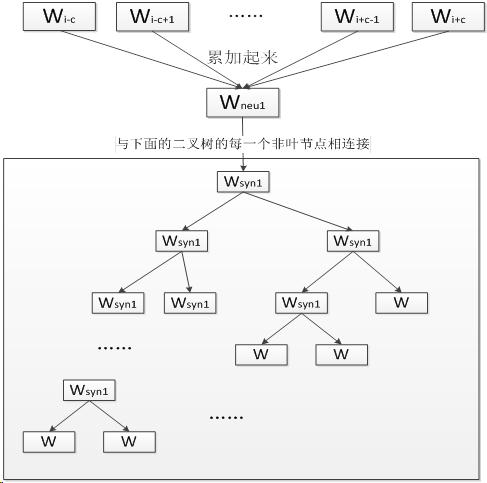
层次Softmax算法结合了Huffman编码，每个词$w$都可以从树的根节点沿着唯一一条路径被访问到。如下图所示，我们可以沿着霍夫曼树从根节点一直走到我们叶子节点的目标词，其中，根节点就是简单求和平均后的词向量。这个霍夫曼树的所有叶子节点就代表了语料库里面的所有词，而且是每个叶子节点对应一个词，不重复。

在word2vec中，采用逻辑回归的方法判断，沿着左子树走为负类1，右子树为正类0

似然函数为：

$$f=\sigma(neu1^T\cdot syn1)$$

实质上就是将每一步的sigmoid求积，neu1表示平均后的词向量，syn1为模型参数，code[j]表示对于目标词w，第j个编码的哈夫曼取值，而我们的目标就是让这个概率最大，通过最大似然的方式求解。

$P(w|Context)=\prod ((f^{1-code[j]}))\cdot ((1- f)^{code[j]})$

$$L=-(1-code[j]logf - code[j]log(1-f))$$

解法选用的是SGD。具体说来就是对每一个样本都进行迭代，但是每个样本只影响其相关的参数，跟它无关的参数不影响。那么梯度就是：

$$Grad_{neu1}=\frac{\partial L}{\partial neu1}=-(1-code[j])\cdot (1-f)\cdot syn1+code[j]\cdot f\cdot syn1=-(1-code[j]-f)\cdot syn1$$

$$Grad_{syn1}=\frac{\partial L}{\partial syn1}=-(1-code[j])\cdot (1-f)\cdot neu1+code[j]\cdot f\cdot neu1=-(1-code[j]-f)\cdot neu1$$

代码如下：

if (hs) for (d = 0; d < vocab[word].codelen; d++) {
    f = 0;
    l2 = vocab[word].point[d] * layer1_size;
    // Propagate hidden -> output
    for (c = 0; c < layer1_size; c++) f += neu1[c] * syn1[c + l2];
    if (f <= -MAX_EXP) continue;
    else if (f >= MAX_EXP) continue;
    else f = expTable[(int)((f + MAX_EXP) * (EXP_TABLE_SIZE / MAX_EXP / 2))];
    // 'g' is the gradient multiplied by the learning rate
    g = (1 - vocab[word].code[d] - f) * alpha;
    // Propagate errors output -> hidden
    for (c = 0; c < layer1_size; c++) neu1e[c] += g * syn1[c + l2];
    // Learn weights hidden -> output
    for (c = 0; c < layer1_size; c++) syn1[c + l2] += g * neu1[c];
}

第二种算法是Negative Sampling，对一个词wij来说，这个词本身是一个正类样本，同时对这个词，还随机抽取了k个负类样本，那么每个词在训练的时候都有k+1个样本，所以要做k+1次SGD。每个样本的负对数似然就是

$f=-label\cdot log f- (1-label) \cdot log (1-f)$

推导过程与上文类似，只是把1 - code[j]替换成label

代码如下：

// NEGATIVE SAMPLING
if (negative > 0) for (d = 0; d < negative + 1; d++) {
    if (d == 0) {
        target = word;
        label = 1;
    } else {
        next_random = next_random * (unsigned long long)25214903917 + 11;
        target = table[(next_random >> 16) % table_size];
        if (target == 0) target = next_random % (vocab_size - 1) + 1;
        if (target == word) continue;
        label = 0;
    }
    l2 = target * layer1_size;
    f = 0;
    for (c = 0; c < layer1_size; c++) f += neu1[c] * syn1neg[c + l2];
    if (f > MAX_EXP) g = (label - 1) * alpha;
    else if (f < -MAX_EXP) g = (label - 0) * alpha;
    else g = (label - expTable[(int)((f + MAX_EXP) * (EXP_TABLE_SIZE / MAX_EXP / 2))]) * alpha;
    for (c = 0; c < layer1_size; c++) neu1e[c] += g * syn1neg[c + l2];
    for (c = 0; c < layer1_size; c++) syn1neg[c + l2] += g * neu1[c];
}

隐层为输入层各变量的加和，因此输入层的梯度其实就是隐层梯度，传播代码如下：

// hidden -> in
for (a = b; a < window * 2 + 1 - b; a++) if (a != window) {
    c = sentence_position - window + a;
    if (c < 0) continue;
    if (c >= sentence_length) continue;
    last_word = sen[c];
    if (last_word == -1) continue;
    for (c = 0; c < layer1_size; c++) syn0[c + last_word * layer1_size] += neu1e[c];
}

Skip-Gram

Skip-Gram和CBOW最大的区别就是表达模型输入输出的方式，对于Skip-Gram来说，训练的任务则变成了由目标词向量预估上下文的2c个词。最终的预估结果会是已知目标词，求上下文的条件概率。

为什么要是用层次化Softmax或Negative Sampling

一般的softmax方法是一个多分类的逻辑回归，分母要对所有词汇表里的单词求和，这使得计算梯度很耗时。

Hierarchical Softmax 使用的办法其实是借助了分类的概念。通过使用哈夫曼编码构造一连串两分类来近似原来的多分类，模型会赋予抽象的中间节点一个合适的向量。这种近似不会带来显著的效果损失，但同时提升了计算性能。

每次分类都会将数据分为两簇

语言模型公式就变成$P(A|C)=p(A|G,C)P(G|C)$.

Negative Sampling也是用二分类近似多分类，随机采样一些负样本，调整模型参数是的模型可以区分。换一个角度来看，就是 Negative Sampling 就稍微选几个词来算算，一般就需要按照词频对应的概率分布来随机抽样。

Reference

https://github.com/danielfrg/word2vec/blob/master/word2vec/includes/word2vec.c

https://blog.csdn.net/zynash2/article/details/81636338

https://blog.csdn.net/mytestmy/article/details/26961315